Can nature design and build for us?


Work by Raphael Kay, Charlie Katrycz, and Kevin Nitiema. More of this type of work (in a refined form) is being completed by Charlie (the expert) towards his PhD thesis (website).
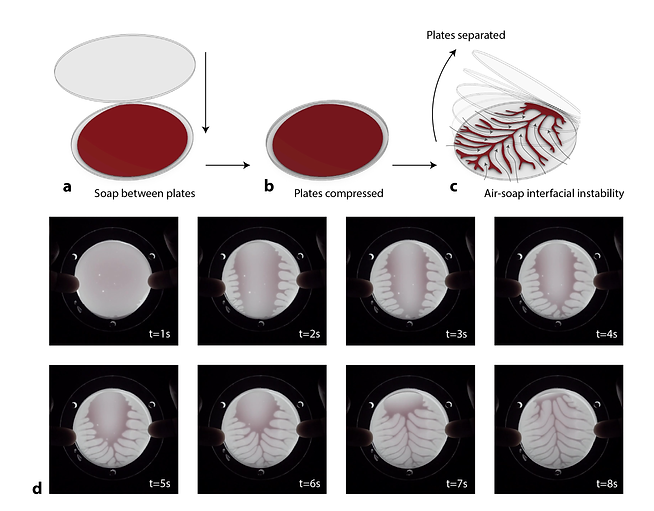
Highly ordered patterns can emerge from nonequilibrium systems. When a fluid of low viscosity, for instance, is driven hard enough into a fluid of high viscosity, an instability will develop at its interface, generating branch-like fractal growth. The fluidic structures that emerge contain meaningful information, and represent a naturally-assembled material solution responsive to a set of spatial and physical constraints.
The above image shows the fluid tunnelling process that occurs when a less viscous fluid (in the above case air) displaces a more viscous fluid (in the above case soap) in porous media.The instability produces a branched fractal pattern similar to the structure of mammalian tissue vascularity (Zamir, 2001), and its design (fractal bifurcation) follows that of an optimal flow pathway for microfluidic networks (Bejan, 2001; Chen et al., 2010; Wu et al., 2010).

The fractal bifurcation pattern produced from the above fluid tunnelling process represents the optimal flow pathway with the maximum flow efficiency for fluidic transport. This network accordingly follows Murray’s Law, stating that when a network branch splits (with radius r), the thickness of the resulting new branches (with radius r1 and r2) is optimized for flow efficiency (Wu et al. 2010). In its simplest form, Murray’s Law states:
r^3 = r1^3 + r2^3
Murray’s Law is obeyed in both the vascular and respiratory systems of animals and in the xylem in plants. It is also obeyed in river branching, as displayed above in g (Roger Beaty).

The above sequence of images illustrates the introduction of a less viscous fluid evenly on both sides of a more viscous fluid, resulting in an even fluid displacement, and an even fractal bifurcation structure.


These (currently unpublished) images represent some early results that suggest that networks we can physically grow (material computation) might have important advantages over networks we can digitally generate (digital computation). They were developed from experiments conducted and designed by Charlie Katrycz (see more here).